Learning

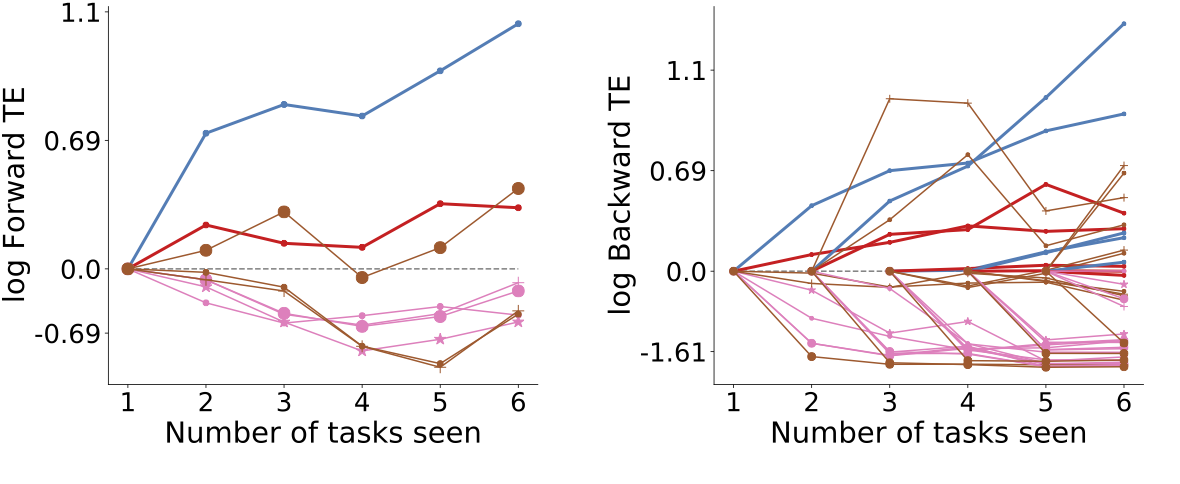
###Lifelong Learning and Beyond
<br>

<center>
![:scale 45%](images/neurodata_blue.png)
</center>

Joshua T. Vogelstein ([jovo@jhu.edu](mailto:jovo@jhu.edu)) | 


[Johns Hopkins University](https://www.jhu.edu/)

---

### What is lifelong learning?

- What is .ye[learning]?
- What is .ye[lifelong learning]?
- What is .ye[beyond]?

---
class:middle

# What is learning?

---

### What is learning (informally)?

<br>
"The acquisition of knowledge or skills through experience, study, or by being taught."

-- Google, 2020

"A computer .ye[program] is set to learn from an .ye[experience] E with respect to some .ye[task] T and some .ye[performance measure] P if its performance on T as measured by P .ye[improves] with experience E."

-- Tom Mitchell, 1997

".ye[$f$] learns from .ye[data] $\mathbf{D}_n$ w.r.t. .ye[tasks] $s$  when its .ye[performance] at $s$ improves due to $\mathbf{D}_n$."

-- jovo, 2020

---

### What is learning (formally)?

---

### Impedance mismatch between informal and formal

- Informal 
  - intuitively pleasing
  - not formalized / operationalized 
- Formal 
  - formalized / operationalized 
  - makes very strong implicit assumptions that are never appropriate
  - only considers one task and one dataset 
  - training and testing distributions assumed to be the same

---

### Our Goal

We desire a formal learning theory framework that:
1. formalizes our intuitive understanding of what is learning 
2. includes  many different kinds of learning scenarios 
3. enables rich theory to provide insight 
4.  guides practice to improve  current AI/ML

---

### Out-Of-Distribution Learning Theory

- We formalize OOD learning theory
- The key insight is decoupling the training data distribution from the test data distribution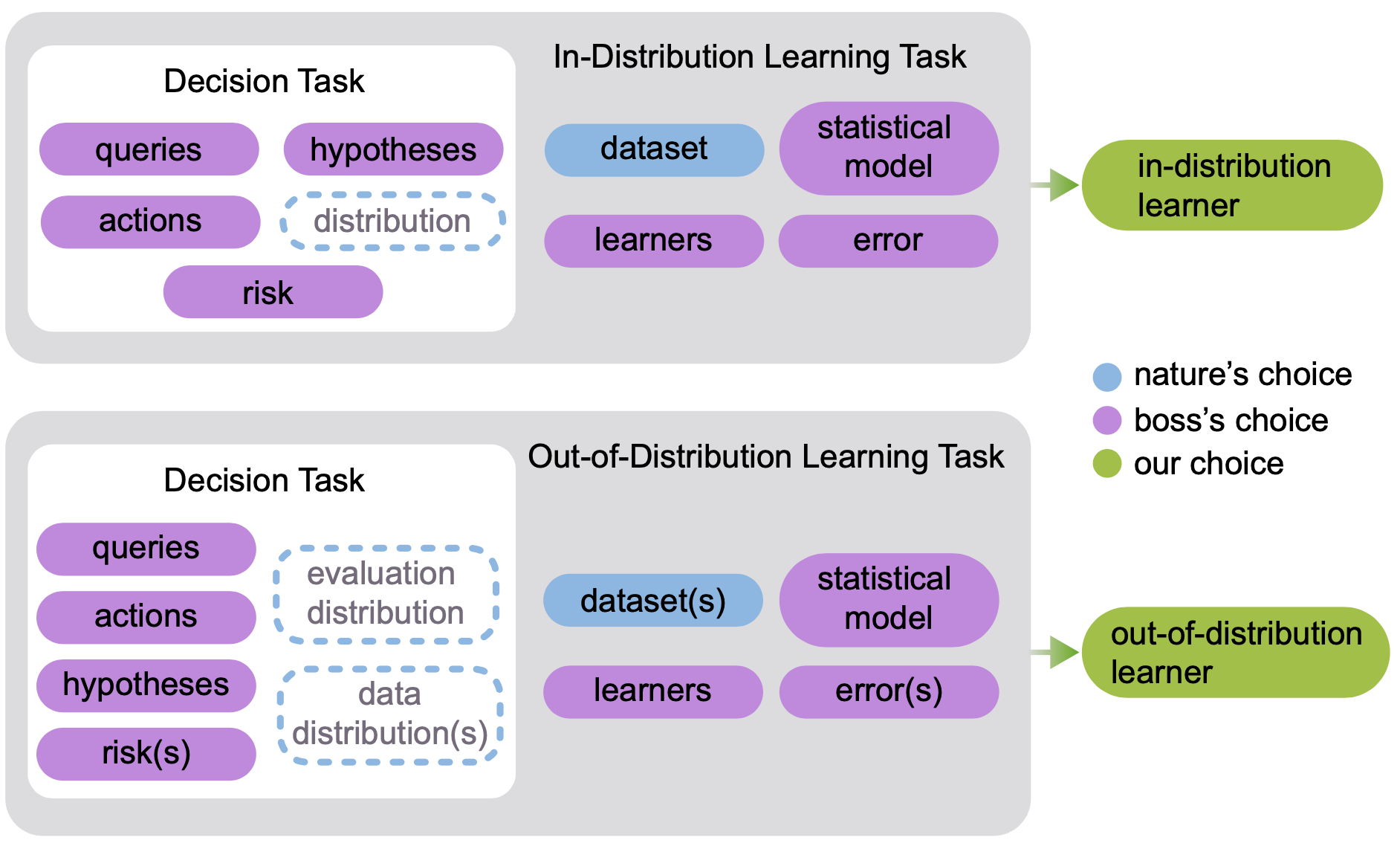

---
### Classical ML Task Setup

- X: observations
- Y: actions/labels 
- S: setting (fixed in classical ML)
- t: indexes samples

![:scale 75%](images/classical-task-setup.png)

---
### Classical ML Task

Minimize error (subject to constraints)

![:scale 100%](images/classical-task-goal.png)

---
### OOD Task

Minimize OOD error (subject to constraints)

![:scale 100%](images/ood-task-goal.png)

Note: 
- S is assumed to be sampled from some distribution over settings 
- train and test distributions are not necessarily the same
- this makes $#*% harder

---
### OK, What is Learning Now?

We introduce .ye[learning efficiency]:

- $ \mathbf{D}^\emptyset $ is the knowledge prior to acquiring data.
- $ \mathbf{D}^1 $ is some training data
- $f$ is the learner 
$$ \text{LE}_f^s(\mathbf{D}^\emptyset, \mathbf{D}^1) = \frac{\mathcal{E}_f^s(\mathbf{D}^\emptyset)}{\mathcal{E}_f^s(\mathbf{D}^1)} $$

<br>
- $f$ learned wrt task $s$ from data $\mathbf{D}^1$ if $ \text{LE} > 1 $, or $\log \text{LE} > 0$.

---

### Revisiting our goals

We desire a formal learning theory framework that:
- [X] formalizes our intuitive understanding of what is learning 
- [ ] includes  many different kinds of learning scenarios 
- [ ] enables rich theory to provide insight 
- [ ]  guides practice to improve  current AI/ML

---

### Transfer Learning
- One task and multiple data sets.
  - $ \mathbf{D}^1 $ is the task data.
  - $ \mathbf{D} $ is all of the data 
- Measure if OOD data helped performance over just task data
$$ \text{LE}_f^s(\mathbf{D}^1, \mathbf{D}) = \frac{\mathcal{E}_f^s(\mathbf{D}^1)}{\mathcal{E}_f^s(\mathbf{D})} $$

<br>
$f$ transfer learned wrt task $s$ using $\mathbf{D} \backslash \mathbf{D}^1$ if $\log \text{LE}_f^s > 0 $.

---

### Multitask Learning
- Multiple tasks and multiple data sets.
  - $ \mathbf{D}^s$ is the data for task $s$.
  - $ \mathbf{D} $ is all of the data.
- Measure transfer learning for each task, 
$$ \text{LE}_f^s(\mathbf{D}^s, \mathbf{D}) = \frac{\mathcal{E}_f^s(\mathbf{D}^s)}{\mathcal{E}_f^s(\mathbf{D})} $$
- $f$ transfer learned for  task  $s$ if $ \log \text{LE}_f^s > 0 $.
- $f$ multitask learned if weighted average of log learning efficiencies is positive.
- multitask learning is just transfer learning across multiple tasks

---

### Lifelong Learning
- Similar to multitask learning
- Sequential rather than batch
- Require computational complexity constraints on hypothesis and learner spaces, $ o(n) $ space and/or $ o(n^2) $ time as upperbounds.
- Everything is streaming: data, queries, actions, error, and tasks. Anything about task can change over time.

---
### Special cases

Each of the previous definitions are all special cases of $LE^s(\mathbf{D}^A, \mathbf{D}^B, f)$, for specific choices of  $\mathbf{D}^A$ and $\mathbf{D}^B$

- Learning: $\mathbf{D}^A=\mathbf{D}\_0$ and $\mathbf{D}^B=\mathbf{D}\_n$.
- Transfer learning: $\mathbf{D}^A=\mathbf{D}^1$ and $\mathbf{D}^B=\mathbf{D}\_n$.
- Multitask learning: for each $t$, $\mathbf{D}^A=\mathbf{D}^s$ and $\mathbf{D}^B=\mathbf{D}\_n$.
- Forward learning: $\mathbf{D}^A=\mathbf{D}^s$ and $\mathbf{D}^B=\mathbf{D}^{< t}$.
- Backward learning: $\mathbf{D}^A=\mathbf{D}^{< t}$ and $\mathbf{D}^B=\mathbf{D}\_n$.

Conjecture: All learning metrics we care about are functions of learning efficiency for a specific $\mathbf{D}^A$ and $\mathbf{D}^B$.

---

### Many different  learning scenarios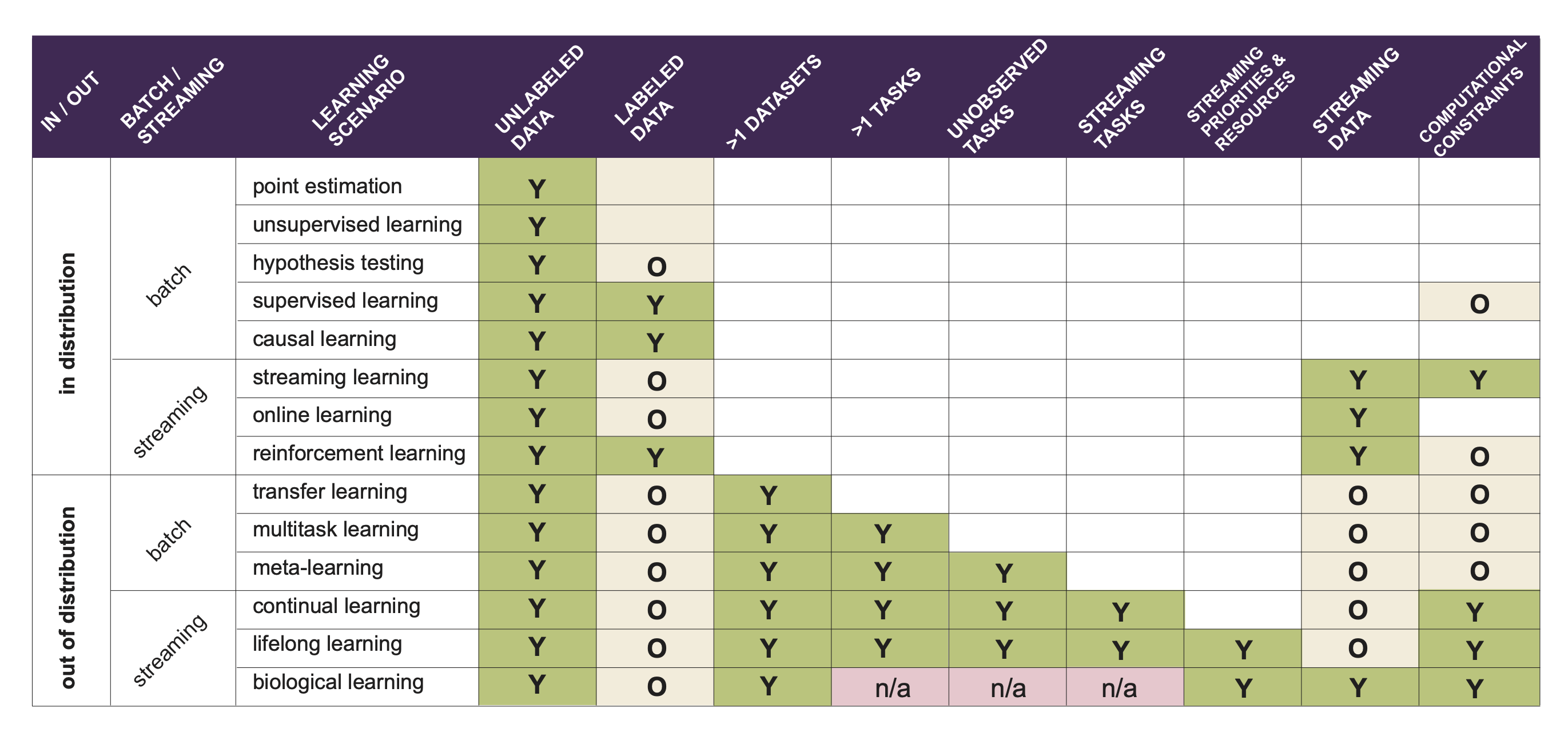

![:scale 100%](images/learning-table.png)

---

### Revisiting our goals

We desire a formal learning theory framework that:
- [X] formalizes our intuitive understanding of what is learning 
- [X] includes  many different kinds of learning scenarios 
- [ ] enables rich theory to provide insight 
- [ ]  guides practice to improve  current AI/ML

---
### Proving novel properties of OOD learning

![:scale 100%](images/weak-ood-learnability.png)

basically, using non-task data to improve performance at all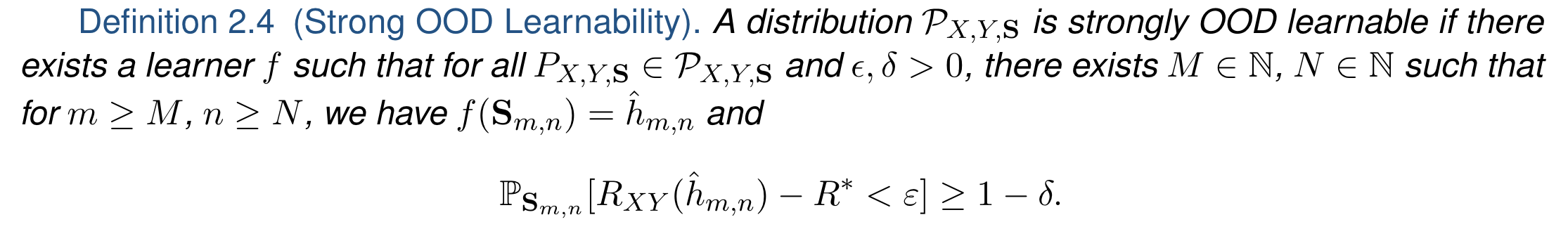

![:scale 100%](images/strong-ood-learnability.png)

basically, using non-task data to perform arbitrarily well

---

### Weak OOD Learner Theorem

Classical theory:
- Weak learning: can do better than chance on some task with sufficient data 
- Strong learning: can do arbitrarily close to optimal on some task with sufficient data
- Weak Learner Theorem: if a problem is weakly learnable, it is also strongly learnable

OOD learning theory
- Training distribution is uncoupled from evaluation distribution

---

### More data is inadequate for LL

Theorem 1: With *only* out-of-distribution data, there exists some problems that are weakly, but not strongly, learnable.

- This implies that OOD learning is different *in kind* from in-distribution learning.
- Lifelong learning is a special case of OOD learning 
- Getting .ye[more] data is *not* guaranteed to improve performance arbitrarily in LL, we need .ye[better] data

---
### Learning efficiency is a fundamental notion of learning

Theorem 2: Weak OOD learnability implies transfer learnability (i.e., learning efficiency > 1).  That is, if one can weakly learn, one can also transfer learn, but not necessarily vice versa.

- This implies that transfer learnability is a fundamental property of learning problems
- In other words, inability to transfer is equivalent to inability to learn at all.

---
### What have we accomplished?

- Showed inadequacy of classical ML framework for OOD learning
- Created a new unifying framework adequate for describing OOD learning
- Proved theorems and results in this new framework

---

### Revisiting our goals

We desire a formal learning theory framework that:
- [X] formalizes our intuitive understanding of what is learning 
- [X] includes  many different kinds of learning scenarios 
- [X] enables rich theory to provide insight 
- [ ]  guides practice to improve  current AI/ML

---
class:middle

# What is lifelong learning?

---

### Defining/Quantifying Learning & Forgetting

![:scale 100%](images/learning-efficiency.png)

Using non-task data to improve performance over what it could achieve using only task data

Key is measuring improvement in performance rather than raw accuracy

---
### What is forward learning?

- Let $n\_t$ be the last occurence of task $t$ in $\mathbf{D}\_n$ 
- Let $\mathbf{D}\_n^{< t} = \lbrace S\_1, S\_2, \ldots, S\_{n_t}  \rbrace$
- .ye[Forward] learning efficiency is the improvement on task $t$ resulting from all data .ye[preceding] task $t$
$$    FLE^s\_{\mathbf{n}}(f) := \frac{\mathcal{E}_f^s(\mathbf{D}^{t}\_n)}{\mathcal{E}_f^s(\mathbf{D}^{< t}\_n)}  $$

<br>

$f$ .ye[forward learns] if $FLE_{\mathbf{n}}(f) > 1$.

---
### What is backward learning?

.ye[Backward] learning efficiency  is the improvement on task $t$ resulting from all data .ye[after] task $t$

$$    BLE^s\_{\mathbf{n}}(f) :=  \frac{\mathcal{E}_f^s(\mathbf{D}^{< t}\_n)}{\mathcal{E}_f^s(\mathbf{D}\_n)}  $$

<br>

$f$ .ye[backward learns] if $BLE_{\mathbf{n}}(f) > 1$.

---
### Learning efficiency factorizes

$$LE^s\_{\mathbf{n}}(f) := FLE^s\_{\mathbf{n}}(f)  \times BLE^s\_{\mathbf{n}}(f) $$

$$ \frac{\mathcal{E}_f^s(\mathbf{D}^{t}\_n)}{\mathcal{E}_f^s(\mathbf{D}\_n)} = \frac{\mathcal{E}_f^s(\mathbf{D}^{t}\_n)}{\mathcal{E}_f^s(\mathbf{D}^{< t}\_n)} \times 
\frac{\mathcal{E}_f^s(\mathbf{D}^{< t}\_n)}{\mathcal{E}_f^s(\mathbf{D}\_n)}  $$

<br>
---
### Lifelong learning is hard: catastrophic forgetting 
![:scale 100%](images/catastrophic.png)
---
### 30 years later... 
![:scale 100%](images/synaptic_intelligence.png)

<br>
And the struggle to not forget continues...
---
### Our claim
A lifelong learning agent should improve on 
<ol style="list-style-type: lower-alpha; padding-bottom: 0;">
  <li style="margin-left:2em">past tasks , i.e., $BLE_{\mathbf{n}}(f) > 1$</li>
  <li style="margin-left:2em">current tasks, i.e., $LE^s_{\mathbf{n}}(f) > 1$ </li>
  <li style="margin-left:2em">future or yet unseen tasks, i.e., $FLE_{\mathbf{n}}(f) > 1$</li>
</ol>

---
### Our approach: ensembling representations

![:scale 100%](images/learning_schema_new.png)
---
### What is lifelong cheating?

- Store every sample you've ever seen 
- Every time we are faced with a new data, just update everything in batch mode 
- Now just run your favorite multitask $f$
- Doing so consumes $\mathcal{O}(n^2)$ resources because $ \sum_{i =1}^n i \approx n^2$

- So, to differentiate lifelong learning from multitask learning requires a particularly efficient algorithm
- $f$ must consume less than quadratic resources as a function of $n$,  $f \in o(n^2)$

---

### A computational taxonomy

| Par.    | → | ←  | capacity | space   | time         | Examples     
| :---:   | :---:  | :---:   | :---:| :---:       | :---:        |                       
| par     | -      | -       | 1    | T           | nT           | EWC        
| par     | -      | -       | 1    | 1           | n            | O-EWC, SI, LwF                   
| par     | +      | -       | 1    | n           | nT           | Total Replay                   
| semipar | +      | 0       | T    | T<sup>2     | nT           | ProgNN 
| semipar | +      | -       | T    | T           | n            | DF-CNN                
| semipar | +      | +       | T    | T + n       | n            | ODIN        
| nonpar  | +      | +       | n    | n           | n            | ODIF

---
### Omnidirectional Algorithms can Transfer Between XOR and XNOR

![:scale 100%](images/xor_xnor_exp.png)
---

## CIFAR 10x10

.pull-left[
- *CIFAR 100* is a popular image classification dataset with 100 classes of images. 
- 500 training images and 100 testing images per class.
- All images are 32x32 color images.
- CIFAR 10x10 breaks the 100-class task problem into 10 tasks, each with 10-class.
]

.pull-right[
<img src="images/l2m_18mo/cifar-10.png" style="position:absolute; left:450px; width:400px;"/>
]
---
### Omnidirectional Algorithms Show Forward Transfer

CIFAR 10x10

![:scale 100%](images/cifar_exp_fte.png)

---
### Omnidirectional Algorithms Uniquely Show Backward Transfer for Each Task
![:scale 100%](images/cifar_exp_bte.png)

---

### Revisiting our goals

---
### Future Directions/ Transitions

- omnidirctional algorithm code continues to improve [http://proglearn.neurodata.io/](http://proglearn.neurodata.io/)
- streaming forest for streaming lifelong learning setup [https://sdtf.neurodata.io](https://sdtf.neurodata.io)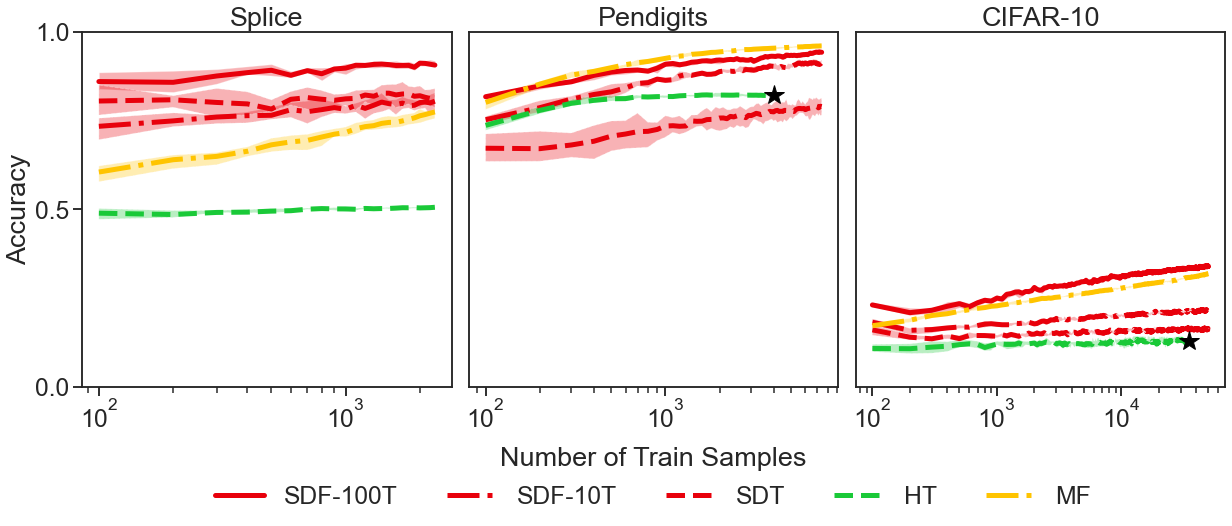
![:scale 80%](images/streaming_forest.png)

---
### Kernel Density Networks/Forests generate well calibrated posteriors 
- [https://github.com/neurodata/kdg](https://github.com/neurodata/kdg)
-  KDG on Guassian XOR simulation data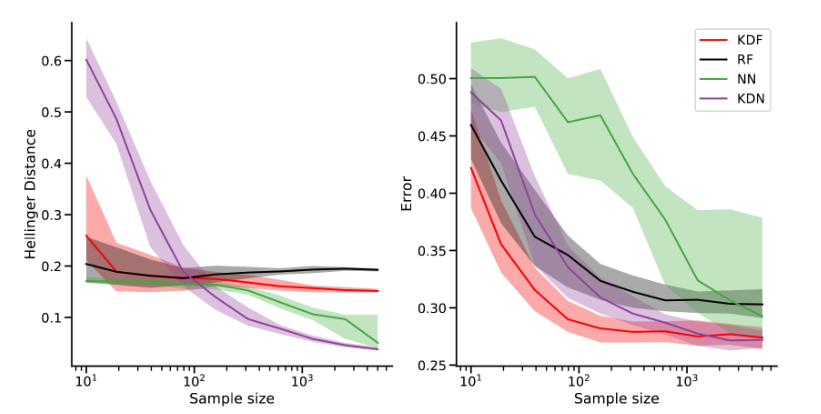

![:scale 100%](images/kdn_kdf.png)
<br>
---
### Deep Networks are the worst model of the mind

<img src=
  "images/nn_rf_jong.gif" 
    alt="jong" 
    width = "700"
    height= "250">  
---
### Acknowledgements

<!-- <div class="small-container">
  <img src="faces/ebridge.jpg"/>
  <div class="centered">Eric Bridgeford</div>
</div>

<div class="small-container">
  <img src="faces/pedigo.jpg"/>
  <div class="centered">Ben Pedigo</div>
</div>

<div class="small-container">
  <img src="faces/jaewon.jpg"/>
  <div class="centered">Jaewon Chung</div>
</div> -->

<div class="small-container">
  <img src="faces/yummy.jpg"/>
  <div class="centered">yummy</div>
</div>

<div class="small-container">
  <img src="faces/family.jpg"/>
  <div class="centered">family</div>
</div>

<div class="small-container">
  <img src="faces/earth.jpg"/>
  <div class="centered">earth</div>
</div>

<div class="small-container">
  <img src="faces/milkyway.jpg"/>
  <div class="centered">milkyway</div>
</div>

##### JHU

<div class="small-container">
  <img src="faces/cep.png"/>
  <div class="centered">Carey Priebe</div>
</div>

<!-- <div class="small-container">
  <img src="faces/bruce_rosen.jpg"/>
  <div class="centered">Bruce Rosen</div>
</div>

<div class="small-container">
  <img src="faces/kent.jpg"/>
  <div class="centered">Kent Kiehl</div>
</div> -->

<!-- <div class="small-container">
  <img src="faces/mim.jpg"/>
  <div class="centered">Michael Miller</div>
</div>

<div class="small-container">
  <img src="faces/dtward.jpg"/>
  <div class="centered">Daniel Tward</div>
</div> -->

<!-- <div class="small-container">
  <img src="faces/vikram.jpg"/>
  <div class="centered">Vikram Chandrashekhar</div>
</div>

<div class="small-container">
  <img src="faces/drishti.jpg"/>
  <div class="centered">Drishti Mannan</div>
</div> -->

<div class="small-container">
  <img src="faces/jesse.jpg"/>
  <div class="centered">Jesse Patsolic</div>
</div>

<div class="small-container">
  <img src="faces/meghana.png"/>
  <div class="centered">Meghana Madhya</div>
</div>

<div class="small-container">
  <img src="faces/hayden.png"/>
  <div class="centered">Hayden Helm</div>
</div>

<div class="small-container">
  <img src="faces/rguo.jpg"/>
  <div class="centered">Richard Gou</div>
</div>

<div class="small-container">
  <img src="faces/ronak.jpg"/>
  <div class="centered">Ronak Mehta</div>
</div>

<div class="small-container">
  <img src="faces/jayanta.jpg"/>
  <div class="centered">Jayanta Dey</div>
</div>

<div class="small-container">
  <img src="faces/will.jpg"/>
  <div class="centered">Will LeVine</div>
</div>

##### Microsoft Research

<div class="small-container">
  <img src="faces/chwh-180x180.jpg"/>
  <div class="centered">Chris White</div>
</div>

<div class="small-container">
  <img src="faces/weiwei.jpg"/>
  <div class="centered">Weiwei Yang</div>
</div>

<div class="small-container">
  <img src="faces/jolarso150px.png"/>
  <div class="centered">Jonathan Larson</div>
</div>

<div class="small-container">
  <img src="faces/brtower-180x180.jpg"/>
  <div class="centered">Bryan Tower</div>
</div>

##### DARPA L2M

{[BME](https://www.bme.jhu.edu/),[CIS](http://cis.jhu.edu/), [ICM](https://icm.jhu.edu/), [KNDI](http://kavlijhu.org/)}@[JHU](https://www.jhu.edu/) | [neurodata](https://neurodata.io)
<br>
[jovo@jhu.edu](mailto:j1c@jhu.edu) | <http://neurodata.io/talks> | [@neuro_data](https://twitter.com/neuro_data)

</div>

---
background-image: url(images/l_and_v.jpeg)

.footnote[Questions?]

---
class: middle 
# .center[Appendix]

---

.small[
### Publications

1. A. Geisa et al. [Towards a theory of out-of-distribution learning](https://arxiv.org/abs/2109.14501), arXiv, 2021. 
1. J. T. Vogelstein et al. [Omnidirectional Transfer for Quasilinear Lifelong Learning](https://arxiv.org/abs/2004.12908), arXiv, 2021.
1. Xu, Haoyin, et al. [Streaming Decision Trees and Forests](https://arxiv.org/abs/2110.08483), arXiv, 2021.
1. C. E. Priebe et al. [Modern Machine Learning: Partition and Vote](https://doi.org/10.1101/2020.04.29.068460), 2020. 
1. R Guo, et al. [Estimating Information-Theoretic Quantities with Uncertainty Forests](https://arxiv.org/abs/1907.00325). arXiv, 2019.
1. R. Perry, et al. [Manifold Forests: Closing the Gap on Neural Networks](https://openreview.net/forum?id=B1xewR4KvH). arXiv, 2019.
1. C. Shen and J. T. Vogelstein. [Decision Forests Induce Characteristic Kernels](https://arxiv.org/abs/1812.00029). arXiv, 2019.
1. M. Madhya, et al. [Geodesic Learning via Unsupervised Decision Forests](https://arxiv.org/abs/1907.02844). arXiv, 2019.
1. M. Madhya, et al. [PACSET (Packed Serialized Trees): Reducing Inference Latency for Tree Ensemble Deployment](https://arxiv.org/abs/2011.05383). arXiv, 2020.

### Conferences 
1. J.T. Vogelstein et al. A biological implementation of lifelong learning in the pursuit of artificial general intelligence.  NAISys, 2020.
2. B. Pedigo et al.  A quantitative comparison of a complete connectome to artificial intelligence architectures. NAISys, 2020.
]

---
### Biological learning is on top

![:scale 100%](images/learning-table.png)
---
### Spoken Digit dataset
.pull-left[
- *Spoken Digit* contains recording from 6 different speakers. 
- Each digit has 50 recordings (3000 total recordings).
- For each recording spectrogram was extracted using using Hanning windows of duration 16 ms with an overlap of 4 ms.
-  The spectrograms were resized down to 28×28. 
]
.pull-right[
<img src="images/spectrogram.png" style="position:absolute; left:500px; width:400px;"/>
]
---
### Omnidirectional Algorithms on Spoken Digit Task

![:scale 105%](images/spoken_digit.png)