Learning

### Lifelong Learning: <br>Theory and Practice and Coresets

PI: Joshua T. Vogelstein, [JHU](https://www.jhu.edu/) <br>
Co-PI: Vova Braverman, [JHU](https://www.jhu.edu/) <br>

Jayanta Dey, Will LeVine, Hayden Helm, Ali Geisa, Ronak Mehta,
Carey E. Priebe

![:scale 30%](images/neurodata_blue.png)

<footer>
  <p> ![:scale 18%](images/jhu.png)
</footer>
---

Biological agents progressively build representations to transfer both forward & backward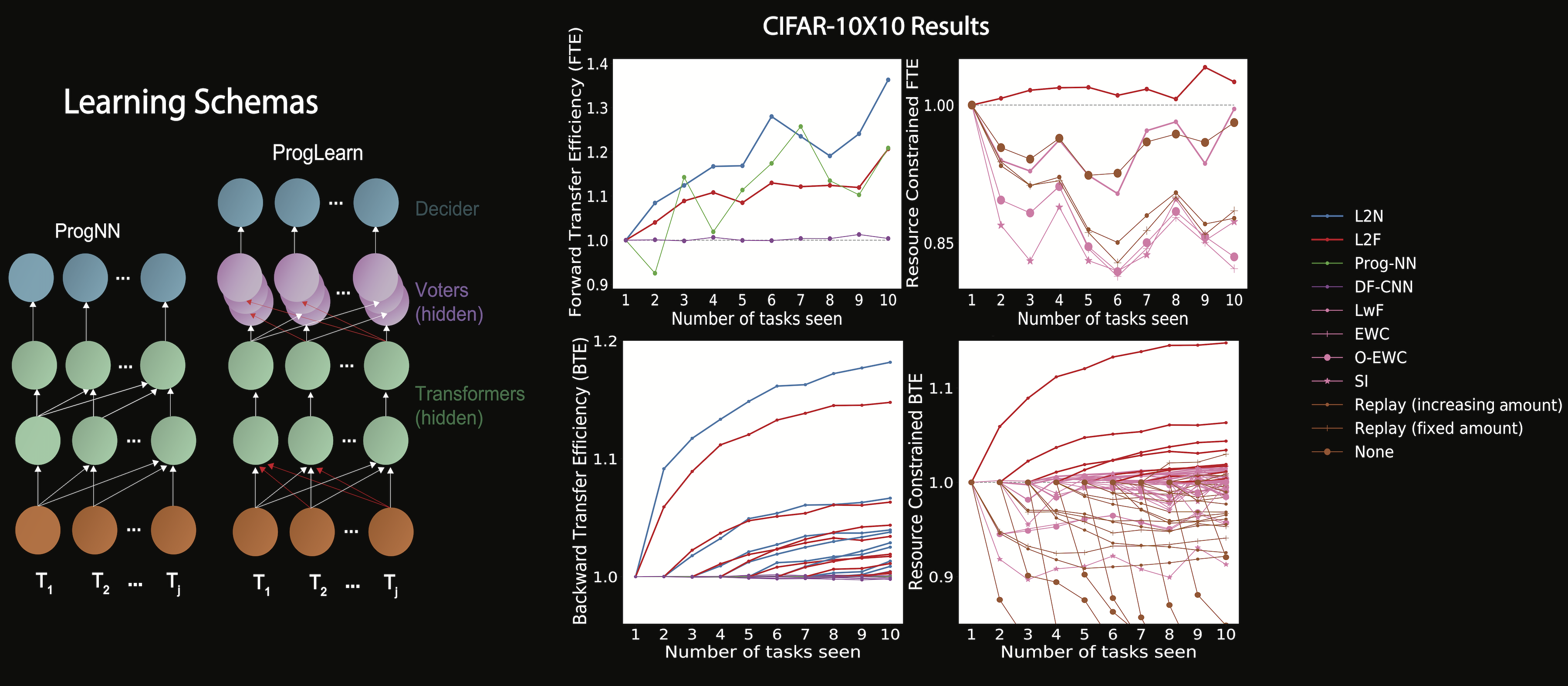

![:scale 90%](images/learning_schema_darpa.png)

1. We learn representations independently for each task, and  ensemble the representations both past and future tasks 
3. We illustrate it achieves SOTA forward, and unique  backward transfer, and uniquely monotonically transfer on CIFAR 10x10
4. It can be applied to any sequential task-aware classification task

<footer>
  <p> ![:scale 18%](images/jhu.png)
</footer>
---

### Potential Collaborations
### [http://proglearn.neurodata.io/](http://proglearn.neurodata.io/)

![:scale 90%](images/proglearn_webpage.png)

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Key  Innovations

1. Modernized statistical decision theory to explicitly incorporate a .ye[learning task] 
2. Introduced .ye[learning efficiency]
3. Formalized and unified .ye[learning metrics]
4. Identified .ye[partition & vote] equivalence of Deep Networks and Decision Forests
5. Developed .ye[Progressive Learning Forests and Networks] 
6. Illustrated the value of .ye[coresets] for lifelong learning (vova)

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Learning Task Definition

| Component | Notation | Examples |
| :--- | :--- | :--- 
| Query Space | $\mathcal{Q}$ | is this a cat?
| Action Space | $\mathcal{A}$ | A,B, ←, →,  ↑, ↓
| Measurement Space | $\mathcal{Z}$ |  8-bit images, 256 x 256
| Statistical Model | $\mathcal{P}$ | Gaussian 
| Hypotheses | $\mathcal{H}$ | linear classifiers
| Risk | $R$ | expected loss
| Algorithm Space | $\mathcal{F}$ | Random Forests
| True & Unknown Distribution | $P$ | $\mu=0$, $\sigma=1$

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### What is learning?

.ye[$f$] learns from .ye[data] $\mathbf{Z}_n$ with respect to .ye[task] $t$  when its .ye[performance] at $t$ improves due to $\mathbf{Z}_n$.

- Define .ye[generalization error] $\mathcal{E}_n(f) := \mathbb{E}_P[R(f(\bold{Z}_n))]$ 
- $\bold{Z}_0$ corresponds to no data. 
- Define .ye[learning efficiency]: $$LE_n(f) := 
\frac{\mathbb{E}_P[R(f(\bold{Z}_0))]}{\mathbb{E}_P[R(f(\bold{Z}_n))]} = 
\frac{\mathcal{E}_0(f)}{\mathcal{E}_n(f)}$$

<br>

$f$ learns from $\mathbf{Z}_n$ with respect to task $t$ when $LE_n(f)  > 1$.

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---
### What is forward learning?

- Let $n\_t$ be the last occurence of task $t$ in $\mathbf{Z}\_n$ 
- Let $\mathbf{Z}\_n^{< t} = \lbrace Z\_1, Z\_2, \ldots, Z\_{n_t}  \rbrace$

.ye[Forward] learning efficiency is the improvement on task $t$ resulting from all data .ye[preceding] task $t$
$$FL^t\_{\mathbf{n}}(f) := \frac{\mathbb{E}[R^t(f(\mathbf{Z}^{t}\_n))]}{\mathbb{E}[R^t(f(\mathbf{Z}^{< t}\_n))]} =\frac{\mathcal{E}\_{Z\_n^t}(f)}{\mathcal{E}\_{Z\_n^{< t}}(f)}.$$

<br>

$f$ .ye[forward learns] if $FL_{\mathbf{n}}(f) > 1$.

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---
### What is backward learning?

.ye[Backward] learning efficiency  is the improvement on task $t$ resulting from all data .ye[after] task $t$

$$    BL^t\_{\mathbf{n}}(f) :=  \frac{\mathbb{E}[R^t(f(\mathbf{Z}^{< t}\_n))]}{\mathbb{E}[R^t(f(\mathbf{Z}\_n))]} =\frac{\mathcal{E}\_{Z\_n^{< t}}(f)}{\mathcal{E}\_{Z\_n}(f)}.  $$

<br>

$f$ .ye[backward learns] if $BL_{\mathbf{n}}(f) > 1$.

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Unification of Learning Metrics

Each of the previous definitions are all special cases of $LE^t(\mathbf{Z}\_A, \mathbf{Z}\_B; f)$, for specific choices of  $\mathbf{Z}\_A$ and $\mathbf{Z}\_B$

- Learning: $\mathbf{Z}\_A=\mathbf{Z}\_0$ and $\mathbf{Z}\_B=\mathbf{Z}\_n$.
- Transfer learning: $\mathbf{Z}\_A=\mathbf{Z}\_n^t$ and $\mathbf{Z}\_B=\mathbf{Z}\_n$.
- Multitask learning: for each $t$, $\mathbf{Z}\_A=\mathbf{Z}\_n^t$ and $\mathbf{Z}\_B=\mathbf{Z}\_n$.
- Forward learning: $\mathbf{Z}\_A=\mathbf{Z}\_n^t$ and $\mathbf{Z}\_B=\mathbf{Z}\_n^{< t}$.
- Backward learning: $\mathbf{Z}\_A=\mathbf{Z}\_n^{< t}$ and $\mathbf{Z}\_B=\mathbf{Z}\_n$.

Conjecture: All learning metrics we care about are functions of learning efficiency for a specific $\mathbf{Z}\_A$ and $\mathbf{Z}\_B$.

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Deep Nets and Decision Forests

![:scale 100%](images/PolytopesFig.svg)

- Both learn convex polytope partitions of feature space, with affine activation functions
- We can easily swap between the two empirically and theoretically

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

#### Progressive Learning Forests and Networks

![:scale 70%](images/learning-schemas-simple.svg)

1. Representers can be forest, networks, etc.
1. Seperate representers learned for each task 
2. Voters leverage both past and future representers

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Key Strength

![:scale 65%](images/L2N-CIFAR-benchmarks.svg)

- SOTA forward transfer
- Unique backward transfer using 500 training samples (SOTA)
- Monotonically increasing backward transfer (SOTA)

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Key Limitations

1. Only works for task-aware (not task-unaware)
1. Only works for classification (not regression)
2. Only batched data (not streaming, not RL)
3. Theorems not yet with dotted i's and crossed t's

<footer>
  <p> 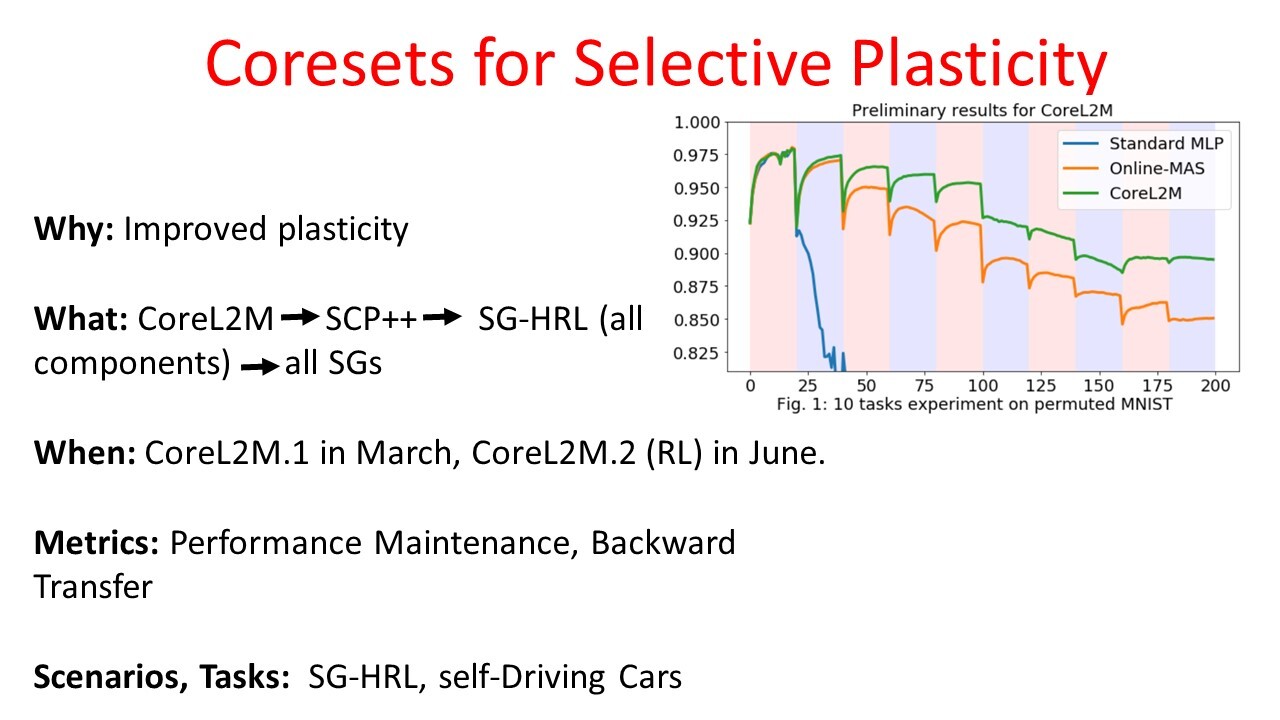![:scale 20%](images/jhu.png)
</footer>
---

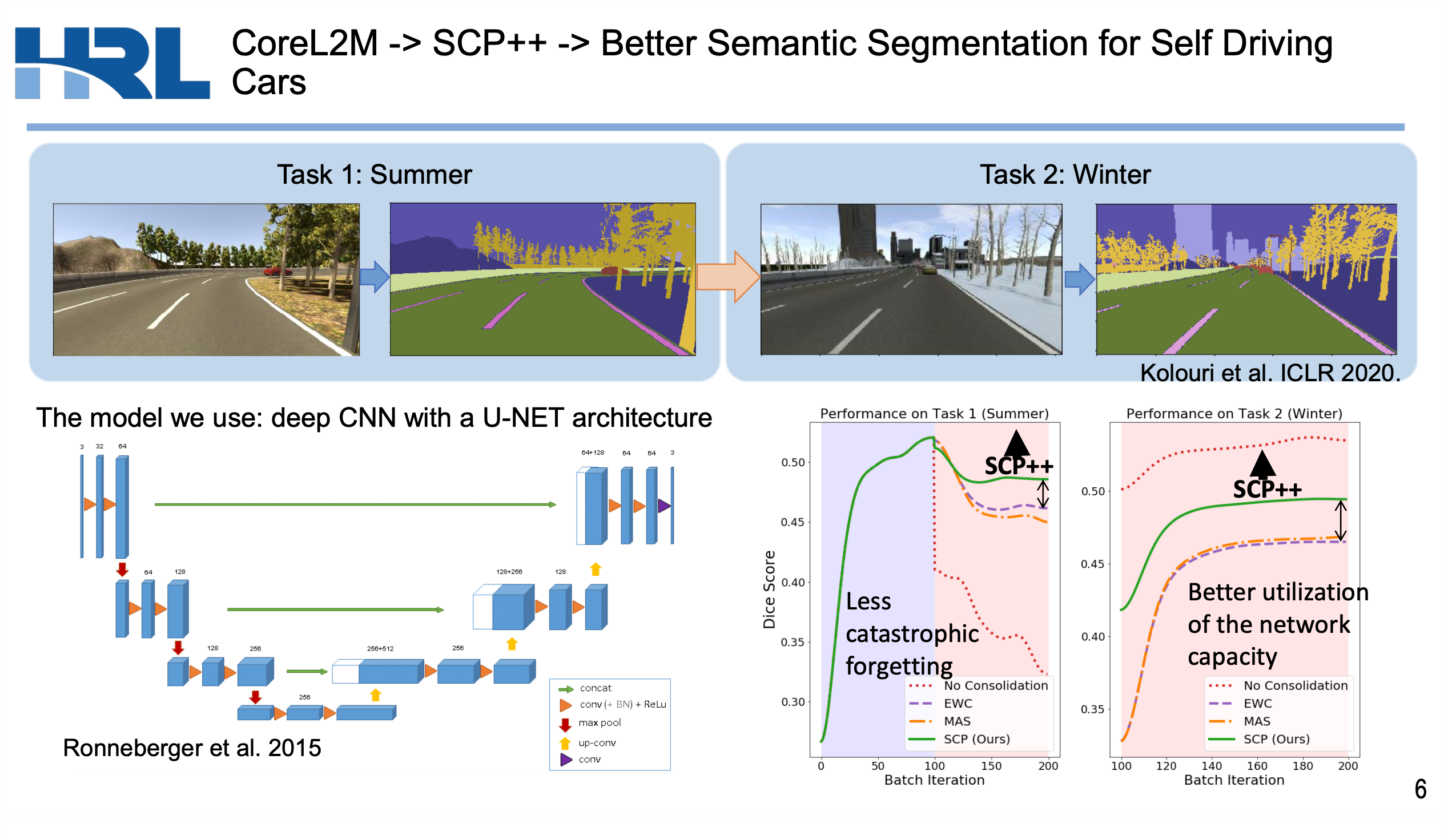![:scale 100%](images/vova_slide1.jpg)

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

![:scale 100%](images/vova_slide2.png)

<footer>
  <p> ![:scale 20%](images/jhu.png)
</footer>
---

### Acknowledgements

<!-- <div class="small-container">
  <img src="faces/ebridge.jpg"/>
  <div class="centered">Eric Bridgeford</div>
</div>

<div class="small-container">
  <img src="faces/pedigo.jpg"/>
  <div class="centered">Ben Pedigo</div>
</div>

<div class="small-container">
  <img src="faces/jaewon.jpg"/>
  <div class="centered">Jaewon Chung</div>
</div> -->

<div class="small-container">
  <img src="faces/yummy.jpg"/>
  <div class="centered">yummy</div>
</div>

<div class="small-container">
  <img src="faces/family.jpg"/>
  <div class="centered">family</div>
</div>

<div class="small-container">
  <img src="faces/earth.jpg"/>
  <div class="centered">earth</div>
</div>

<div class="small-container">
  <img src="faces/milkyway.jpg"/>
  <div class="centered">milkyway</div>
</div>

##### JHU

<div class="small-container">
  <img src="faces/cep.png"/>
  <div class="centered">Carey Priebe</div>
</div>

<!-- <div class="small-container">
  <img src="faces/bruce_rosen.jpg"/>
  <div class="centered">Bruce Rosen</div>
</div>

<div class="small-container">
  <img src="faces/kent.jpg"/>
  <div class="centered">Kent Kiehl</div>
</div> -->

<!-- <div class="small-container">
  <img src="faces/mim.jpg"/>
  <div class="centered">Michael Miller</div>
</div>

<div class="small-container">
  <img src="faces/dtward.jpg"/>
  <div class="centered">Daniel Tward</div>
</div> -->

<!-- <div class="small-container">
  <img src="faces/vikram.jpg"/>
  <div class="centered">Vikram Chandrashekhar</div>
</div>

<div class="small-container">
  <img src="faces/drishti.jpg"/>
  <div class="centered">Drishti Mannan</div>
</div> -->

<div class="small-container">
  <img src="faces/meghana.png"/>
  <div class="centered">Meghana Madhya</div>
</div>

<div class="small-container">
  <img src="faces/ronak.jpg"/>
  <div class="centered">Ronak Mehta</div>
</div>

<div class="small-container">
  <img src="faces/jayanta.jpg"/>
  <div class="centered">Jayanta Dey</div>
</div>

<div class="small-container">
  <img src="faces/will.jpg"/>
  <div class="centered">Will LeVine</div>
</div>

<div class="small-container">
  <img src="faces/hayden.png"/>
  <div class="centered">Hayden Helm</div>
</div>

<div class="small-container">
  <img src="faces/rguo.jpg"/>
  <div class="centered">Richard Gou</div>
</div>

<div class="small-container">
  <img src="faces/alig.jpg"/>
  <div class="centered">Ali Geisa</div>
</div>

##### Microsoft Research

<div class="small-container">
  <img src="faces/chwh-180x180.jpg"/>
  <div class="centered">Chris White</div>
</div>

<div class="small-container">
  <img src="faces/weiwei.jpg"/>
  <div class="centered">Weiwei Yang</div>
</div>

<div class="small-container">
  <img src="faces/jolarso150px.png"/>
  <div class="centered">Jonathan Larson</div>
</div>

<div class="small-container">
  <img src="faces/brtower-180x180.jpg"/>
  <div class="centered">Bryan Tower</div>
</div>

##### DARPA L2M: All code open source and reproducible from [proglearn.neurodata.io/](http://proglearn.neurodata.io/)

{[BME](https://www.bme.jhu.edu/),[CIS](http://cis.jhu.edu/), [ICM](https://icm.jhu.edu/), [KNDI](http://kavlijhu.org/)}@[JHU](https://www.jhu.edu/) | [neurodata](https://neurodata.io)
<br>
[jovo@jhu.edu](mailto:j1c@jhu.edu) | <http://neurodata.io/talks> | [@neuro_data](https://twitter.com/neuro_data)

</div>

---
background-image: url(images/l_and_v.jpeg)

.footnote[Questions?]